CS 180 Project 3
Part 1. Defining Correspondences
I used portraits of Matt Bomer and Henry Cavill, as shown below. I plotted correspondences for various features of their faces, triangularized them using the Delauney function on the midpoints of each corresponding pairs of points.
 |
 |
|---|---|
 |
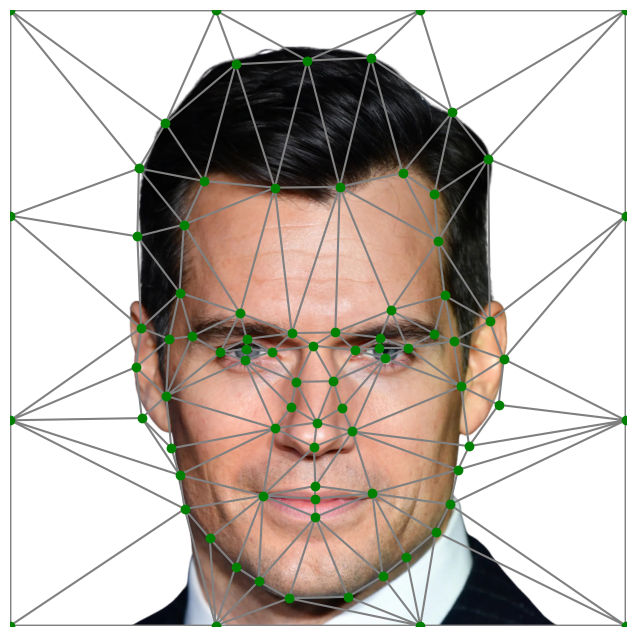 |
Part 2. Computing the "Mid-way Face"
To compute the midway face, I performed affine transformations that would transform each corresponding triangle to the midway triangle. More specifically:
- For each triangle, I found the affine transformation matrix that would transform the midway triangle to the corresponding source images.
- Then, for each pixel in the triangle, I would interpolate the pixel values in the original images to get the morphed images.
- Finally, I would take the average of the images to get the morphed image

Part 3. The Morph Sequence
To animate this transformation, I repeated this process for 45 in-between steps, where the middle points would be (1-alpha) * bomer_pts + alpha * cavill_pts, where alpha would vary from 0 to 1 throughout this whole process. Similarly, the result image would be a weighted average, specifically (1-alpha) * morphed_bomer + alpha * morphed_cavill.

Part 4: The "Mean Face" of a Population
I utilized the IMM Face Database, which comprises of 240 images of 40 different people, 7 women and 33 men. Each person has 6 images in various poses/lighting. For this part, I decided to use only the male images with a neutral expression. They were also annotated using 58 landmarks for their eyes, nose, mouth, jaw, and eyebrows. I also appended 4 more landmarks for the corners of the image so the triangulation would cover the entire image and not just the face. Pictured are the original images I used.
I took the mean of all of these points, morphed each image onto the average set of features, and overlayed them all on top of each other.
 |
 |
|---|
These are some of the faces mapped onto the mean face. Notice that quite a few of the heads are warped since there are no features for their hairline or upper face.

I also morphed myself into the avg of the dataset, and morphed the average onto my own geometry.
 |
 |
 |
|---|
Part 5: Caricatures: Extrapolating from the mean
By taking the difference between my geometry and the mean geometry, scaling it by some positive factor, and then adding it back to my original points, I was able to exaggerate some of my features. More specifically, for some alpha > 0, I morphed my face onto the points: my_pts + alpha * (my_pts - mean_pts). The results are shown below.
 |
 |
 |
|---|
Part 6: Bells and Whistles
I performed PCA on a larger subset of the dataset. This time, I included both men and women in the dataset, and used 3 different poses for each person:
- Neutral face, diffuse light
- Happy face, diffuse light
- Neutral face, harsh light on right side of face.
I used 25 features in total. These were the eigenfaces.

Pictured below are a few of the triplets of original images, reconstructed images, and the caricaturized versions of the reconstruction.

Finally, this is a reconstruction of myself. It is much worse, likely due to misalignment and multiple features being different.
